中国科学院物理研究所
北京凝聚态物理国家研究中心
T03组供稿
第36期
2011年12月21日
硅烯中的量子自旋霍尔效应
近几年来,拓扑绝缘体的研究在世界范围内飞速发展,并成为凝聚态物理研究中的一个热点领域。从电子能带结构上来说,拓扑绝缘的体电子态是有能隙的绝缘态;而它的表面(对三维体系)或者边缘(对二维体系)电子态则是零能隙有手性的金属态。这类拓扑绝缘态由材料的强自旋轨道耦合引起,具有时间反演对称性。拓扑绝缘体的重要性在于存在由时间反演不变对称性所保护的表面态。并且该表面态是由能带结构的内在拓扑性质所决定,不容易受到缺陷、杂质等外界环境的影响。量子自旋霍尔效应即二维的拓扑绝缘体最早由Pennsylvania 大学的Kane和Mele在单层石墨烯样品中提出【Phys.Rev.Lett.95, 226801(2005);95,146802 (2005)】。但中国科学院物理研究所/北京凝聚态物理国家实验室(筹)姚裕贵研究员等随后的工作表明由于自旋轨道耦合在石墨烯中打开的能隙仅μeV量级,大小可忽略不计,由此可以断定在石墨烯中很难观测到量子化的自旋霍尔效应【Phys. Rev. B 75, 041401(R) (2007)】。很快斯坦福大学的张守晟研究组提出在HgTe/CdTe 量子阱体系可以实现量子自旋霍尔效应【Science 314,1757(2006)】,并在非常短的时间内被德国的Laurens Molenkamp研究组实验证实【Science 318,766(2007)】。在量子自旋霍尔样品中,由于强自旋轨道耦合,载流子只能沿着样品边缘传输,并且是无耗散的,可望应用于下一代自旋电子学器件。
根据拓扑能带理论,拓扑绝缘体和普通绝缘体可以由拓扑不变量Z2来区分。Z2可以用晶体中BLOCH态的贝里(Berry)相位来刻画。量子力学中的贝里(Berry)相位自1984年发现以来,在诸多领域中已得到了广泛的应用,在凝聚态领域中,贝里相位则深刻影响到固体的电子动力学行为。姚裕贵研究员在此相关领域进行了多年的系统研究,并取得了许多重要成果。如利用第一性原理方法精确地计算了贝里相位对反常霍尔效应(PRL 2004,2006a)、自旋霍尔效应(PRL 2005a, PRL 2005b)、反常热电效应(PRL 2006b)等的影响。在多年的研究基础上,最近他在第一性原理程序中首次实现了拓扑不变量Z2的普适计算,进而可以直接判断一个材料是否为拓扑绝缘体。这个计算方法适用于包括空间反演破缺的体系,将成为寻找拓扑绝缘体新材料的强有力工具【arXiv: 1107.2679】。利用此程序,他们已经预测了Half-Heusler [Phys. Rev. Lett. 105, 096404 (2010)]和黄铜矿[Phys. Rev. Lett. 106, 016402 (2011)]两个体系中可能存在大量拓扑绝缘体。
最近,中科院物理所/北京凝聚态物理国家实验室(筹)T03组的姚裕贵研究员以及博士生刘铖铖、冯万祥采用第一性原理系统地研究硅烯的晶体结构、稳定性、能带拓扑和自旋轨道耦合打开的能隙。他们利用绝热连续性以及直接计算拓扑不变量Z2,预言了在硅烯中可以实现量子自旋霍尔效应,具有远大于石墨烯的1.55meV的自旋轨道耦合能隙,对应于18K。 此外,该小组还研究了二维的六角锗体系,虽然蜂窝结构的二维锗在实验上尚未合成,但他们预言了在该体系中也可实现量子自旋霍尔效应,具有23.9meV的自旋轨道耦合能隙,对应于277K。进一步通过紧束缚方法,姚裕贵研究员、博士生刘铖铖和博士后江华还给出了上述体系的低能有效哈密顿量,并阐明了由于起伏结构,硅烯中有效的自旋轨道耦合包含了一阶的自旋轨道耦合相互作用,这是导致硅烯中存在相当大能隙的根本物理原因。这一点完全不同于平面结构的石墨烯,其有效的自旋轨道耦合只包含了二阶的自旋轨道耦合相互作用。
硅烯具有类似于石墨烯的蜂窝状结构,不同之处在于硅烯的蜂窝状结构是有起伏的。其结构见图1。该类新奇的材料在试验上已经合成,并被证实具有石墨烯类似的电子结构【Appl. Phys. Lett. 96,183102 (2010); Appl. Phys. Lett. 96, 261905 (2010); Appl. Phys. Lett. 97, 223109 (2010).】。硅烯可以非常好地与当今的硅基半导体工艺兼容,这是其他量子自旋霍尔体系所不具有的。此外由于结构相似性,石墨烯的所有奇异性质几乎都可能移植到硅烯中,可以预期硅烯在将来有着广泛的应用前景。
本工作发表在Phys. Rev. Lett. 107, 076802 (2011),Phys. Rev. B 84, 195430 (2011), 并得到了国家自然科学基金委、科技部和科学院的资助。
相关参考文献:
1. C. C. Liu, W. X. Feng, Y. G. Yao “Quantum Spin Hall Effect in Silicene and Two-Dimensional Germanium”, Phys. Rev. Lett. 107, 076802 (2011).
2. C. C. Liu, H. Jiang, Y. G. Yao “Low-energy effective Hamiltonian involving spin-orbit coupling in Silicene and Two-Dimensional Germanium and Tin”, Phys. Rev. B 84, 195430 (2011).
根据拓扑能带理论,拓扑绝缘体和普通绝缘体可以由拓扑不变量Z2来区分。Z2可以用晶体中BLOCH态的贝里(Berry)相位来刻画。量子力学中的贝里(Berry)相位自1984年发现以来,在诸多领域中已得到了广泛的应用,在凝聚态领域中,贝里相位则深刻影响到固体的电子动力学行为。姚裕贵研究员在此相关领域进行了多年的系统研究,并取得了许多重要成果。如利用第一性原理方法精确地计算了贝里相位对反常霍尔效应(PRL 2004,2006a)、自旋霍尔效应(PRL 2005a, PRL 2005b)、反常热电效应(PRL 2006b)等的影响。在多年的研究基础上,最近他在第一性原理程序中首次实现了拓扑不变量Z2的普适计算,进而可以直接判断一个材料是否为拓扑绝缘体。这个计算方法适用于包括空间反演破缺的体系,将成为寻找拓扑绝缘体新材料的强有力工具【arXiv: 1107.2679】。利用此程序,他们已经预测了Half-Heusler [Phys. Rev. Lett. 105, 096404 (2010)]和黄铜矿[Phys. Rev. Lett. 106, 016402 (2011)]两个体系中可能存在大量拓扑绝缘体。
最近,中科院物理所/北京凝聚态物理国家实验室(筹)T03组的姚裕贵研究员以及博士生刘铖铖、冯万祥采用第一性原理系统地研究硅烯的晶体结构、稳定性、能带拓扑和自旋轨道耦合打开的能隙。他们利用绝热连续性以及直接计算拓扑不变量Z2,预言了在硅烯中可以实现量子自旋霍尔效应,具有远大于石墨烯的1.55meV的自旋轨道耦合能隙,对应于18K。 此外,该小组还研究了二维的六角锗体系,虽然蜂窝结构的二维锗在实验上尚未合成,但他们预言了在该体系中也可实现量子自旋霍尔效应,具有23.9meV的自旋轨道耦合能隙,对应于277K。进一步通过紧束缚方法,姚裕贵研究员、博士生刘铖铖和博士后江华还给出了上述体系的低能有效哈密顿量,并阐明了由于起伏结构,硅烯中有效的自旋轨道耦合包含了一阶的自旋轨道耦合相互作用,这是导致硅烯中存在相当大能隙的根本物理原因。这一点完全不同于平面结构的石墨烯,其有效的自旋轨道耦合只包含了二阶的自旋轨道耦合相互作用。
硅烯具有类似于石墨烯的蜂窝状结构,不同之处在于硅烯的蜂窝状结构是有起伏的。其结构见图1。该类新奇的材料在试验上已经合成,并被证实具有石墨烯类似的电子结构【Appl. Phys. Lett. 96,183102 (2010); Appl. Phys. Lett. 96, 261905 (2010); Appl. Phys. Lett. 97, 223109 (2010).】。硅烯可以非常好地与当今的硅基半导体工艺兼容,这是其他量子自旋霍尔体系所不具有的。此外由于结构相似性,石墨烯的所有奇异性质几乎都可能移植到硅烯中,可以预期硅烯在将来有着广泛的应用前景。
本工作发表在Phys. Rev. Lett. 107, 076802 (2011),Phys. Rev. B 84, 195430 (2011), 并得到了国家自然科学基金委、科技部和科学院的资助。
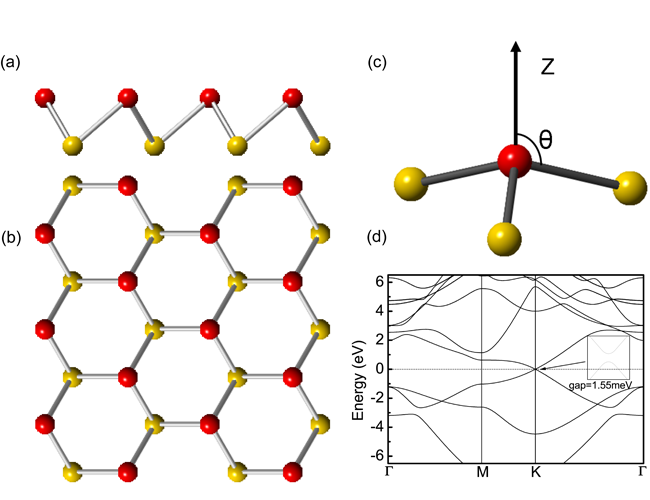 |
| 图1 硅烯的晶体结构和能带图。(a),(b)分别为侧视图和俯视图。(c)定义了一个起伏角度。(d) 能带图。放大的部分为由于自旋轨道耦合作用在狄拉克点打开的能隙结构。 |
相关参考文献:
1. C. C. Liu, W. X. Feng, Y. G. Yao “Quantum Spin Hall Effect in Silicene and Two-Dimensional Germanium”, Phys. Rev. Lett. 107, 076802 (2011).
2. C. C. Liu, H. Jiang, Y. G. Yao “Low-energy effective Hamiltonian involving spin-orbit coupling in Silicene and Two-Dimensional Germanium and Tin”, Phys. Rev. B 84, 195430 (2011).

