最近，中国科学院物理研究所/北京凝聚态物理国家实验室刘伍明研究组在N个二能级原子和单模微腔耦合的光学系统中观测到光子的戈德斯通模和希格斯模。他们使用1/J展开和精确对角化两种方法，分别计算了这个光学系统的戈德斯通模和希格斯模的能量，和它们相应的光谱权重，以及反向旋转波的效应。
    当物理系统所遵守的自然定律具有某种对称性，而物理系统本身并不具有这种对称性，则称此现象为自发对称性破缺。对称性自发破缺后，会产生两种类型的激发粒子：一种无质量，被称为戈德斯通（Goldstone）粒子，这种粒子也被称为戈德斯通模；另一种有质量，被称为希格斯（Higgs）粒子，这种粒子也被称为希格斯模。无质量的戈德斯通模已经在量子反铁磁体、超流和冷原子系统中检测到。德国科学家Ulf Bissbort等人首次在光晶格冷原子系统中的强相互作用玻色子里检测到有质量的希格斯模。希格斯模也可以用超导中的拉曼散射和弹性中子散射实验检测。由德国科学家Manuel Endres等人于2012年在二维光晶格的冷原子系统中检测到希格斯模并且计算了它的衰变几率。实验上在陷俘系统中检测到希格斯模的离散性质。在相对论量子场论中人们已经熟知由希格斯机制可以推导出各种基本粒子的质谱。尽管人们已经预言了许多基本粒子的质量，但是原始的有质量的希格斯粒子依然是难以确定的，直到最近在大型强子对撞机所做的质量为125GeV和宽度为6MeV的实验中它才最终被确定下来。
    中国科学院物理研究所/北京凝聚态物理国家实验室（筹）T05组刘伍明研究员、博士生喻益湘和首都师范大学叶锦武教授合作，研究了N个二能级原子和单模微腔耦合的光学系统，通过减少原子数观察到戈德斯通模和希格斯模。他们使用1/J展开和精确对角化两种方法，分别计算了超辐射相位里的戈德斯通模和希格斯模的能量，和它们相应的光谱权重，其中J=N/2 （J是系统的总自旋），N是有限的。他们发现随着二能级原子数N减少到N=2时，由以上两种方法得到的结果都吻合。这表明用多体理论研究拥有大量粒子数的凝聚态系统的方法，也可以用来研究只有几个粒子的凝聚态系统。他们还使用1/J展开的方法研究了反向旋转波的效应，发现对几个原子来说，如果反向旋转波中原子与光子的耦合参数和旋转波中的原子-光子的耦合参数之比g'/g<1/3，在反向旋转波中有限尺寸效应将占主导。他们提出了一些减少临界耦合强度g_c的方案，使得这两种模式可以在一些方便光学测量的实验系统中观测到。
    相关研究得到中国科学院、国家自然科学基金委员会和科技部的支持。该结果发表在2013年12月11日出版的Scientific Reports上 【Scientific Reports. 3, 3476 (2013)】。
    相关链接：
http://www.nature.com/srep/2013/131211/srep03476/full/srep03476.html

图1（a）微腔中N个二能级原子与单模光子的耦合图，图中ωa是微腔中光子的频率，u是原子间的相互作用参数，g是原子与光子间的耦合参数。调整原子间的相互作用u可以减少临界耦合参数gc。（b）当二能级原子数N=3时，用1/J展开的方法得到的Mandel因子QM（红色）和用精确对角化方法得到的Mandel因子QM（蓝色）之对比。在超辐射相位中，含有Mandel因子QM的态是一个数字压缩态。

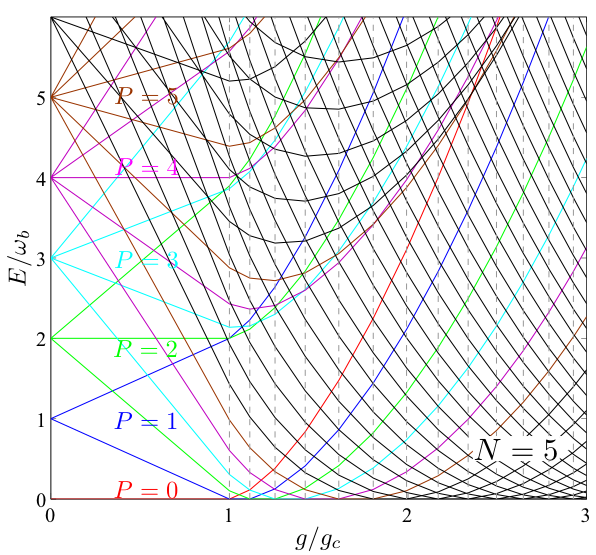图2，在二能级原子数N=5和共振条件ωa=ωb下，用精确对角化方法得到的系统能量E随原子与光子之间的耦合参数与临界耦合参数之比g/gc的变化，ωa是微腔中光子的频率，ωb是两个原子的能量差。由精确对角化方法得到的系统能量\(E\left(l,m\right)=\left(l+1/2\right) \hbar E_H+\frac{D}{2}\left(m+l-\alpha\right)\)，式中EH是希格斯模的能量，D是相位弥散常数，m=-P，-P+1，…是给定总激发数P后的磁量子数，l是朗道能级。当l=0，m=0时得到基态能，而图中的E表示已经减去基态能的系统能量。图中曲线代表能量E，不同颜色的曲线E对应不同的总激发数P。总激发数\(p=a^ \dagger a+b^ \dagger b\)，其中a代表光子算子，b代表原子算子。图中的虚线对应g的临界值，基态中的总激发数P由1开始增长。

图3 （a）用1/J展开的方法得到的戈德斯通模的能量\(E_G\left(\alpha=-1/2\right)=D\left(g\right)=\frac{2\omega_ag^2}{E^2_HN}\)（红线）和用精确对角化方法得到的戈德斯通模的能量\(E_G=E^{p+1}_0-E^p_0\)（蓝线）之对比，其中α是表征二能级原子泡利矩阵σα的分量，α=1，2，3。\(D\left(g\right)=\frac{2\omega_ag^2}{E^2_HN}\)是相位弥漫常数，式中ωa是微腔中光子的频率，g是原子与光子之间的耦合参数，EH是希格斯能量，二能级原子数N=1，2，3，5。由图可以看出，当总激发数P很小时，用1/J展开的方法得到的戈德斯通模的能量EG和用精确对角化方法得到的EG的变化趋势基本吻合。（b）当二能级原子数N=3时，用1/J展开的方法得到的戈德斯通模的光谱权重\(C_G=\lambda^2_a-\frac{\omega_a}{4E_H}\left(\frac{\omega_a+\omega_b}{E_H}+1\right)^2+\left(1-\alpha\gamma/2\right)\)（红色）和用精确对角化得到的戈德斯通模的光谱权重\(C_G= \left| \langle P+1,l=0 \arrowvert {a}^{\dagger} \arrowvert P,l=0 \rangle \right|^{2} \)（蓝色）之对比，式中λa是原子算子b和光子算子a变换到极坐标后对应的参数，ωb是两个原子的能量差，γ是原子算子和光子算子变换到极坐标后，再变换到±模后的相互作用的耦合参数。\(a^\dagger\)是光子算子的共轭。从走势上我们可以看出，这两种方法得到的结果基本一样。

图4，（a）当二能级原子数N=3时，除去刚开始的几步外，用精确对角化方法得到的结果\(E_0=E^{p+1}_1-E^p_0\)（蓝线）满足解析关系E0=EH+EG（红线表示希格斯模的能量EH）。（b）当二能级原子数N=3时，用1/J展开的方法得到的光学模的光谱权重\(C_0\left(g\right)=\frac{\omega_a}{4E_H}\left(\frac{\omega_a+\omega_b}{E_H}+1\right)^2\)（红色）和用精确对角化方法得到的光学模的光谱权重\(C_0 \left(g \right)= \left| \langle P+1,l=1 \arrowvert {a}^{\dagger} \arrowvert P,l=0 \rangle \right|^{2}\)（蓝色）之对比，式中ωa是微腔中光子的频率，ωb是两个原子的能量差，P是总激发数，\(a^\dagger\)是光子算子的共轭。

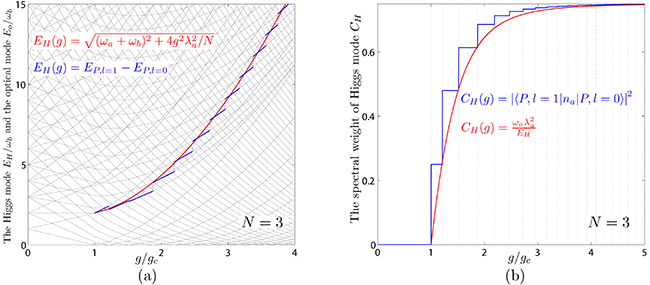图5，（a）当二能级原子数N=3时，用1/J展开的方法得到的希格斯能量\(E_H\left(g\right)=\sqrt{\left(\omega_a+\omega_b\right)^2+4g^2\lambda_a/N}\)（红色）和用精确对角化方法得到的希格斯能量\(E_H\left(g\right)=E^p_1-E^p_0\)（蓝色）之对比，式中ωa是微腔中光子的频率，ωb是两个原子的能量差，g是原子与光子之间的耦合参数，λa是原子算子b和光子算子a变换到极坐标后对应的参数。（b）当二能级原子数N=3时，用1/J展开的方法得到的希格斯的光谱权重\(C_H\left(g\right)=\frac{\omega_a\lambda^2_a}{E_H}\)（红色）和用精确对角化方法得到的希格斯的光谱权重\(C_H \left(g \right)= \left| \langle P+1,l=1 \arrowvert {n}_{a} \arrowvert P,l=0 \rangle \right|^{2}\)（蓝色）之对比，其中P是总激发数，na是光子数。与图3一起，可以看出用1/J展开的方法和用精确对角化方法得到的关于戈德斯通模和希格斯模的结果都基本吻合。