中国科学院物理研究所
北京凝聚态物理国家研究中心
T03组供稿
第10期
2015年04月07日
理论预言的拓扑Weyl半金属:TaAs家族
1928年狄拉克提出描述相对论电子态的狄拉克方程。第二年,H. Weyl指出,当质量为零时,狄拉克方程描述的是一对重叠在一起的具有相反手性的新粒子,这就是Weyl费米子。但是80多年过去了,人们一直没有能够在实验中观测到Weyl费米子。中微子曾经被认为是Weyl费米子,但是后来发现中微子其实是有质量的。近年来,拓扑绝缘体,尤其是拓扑半金属领域的飞速发展为Weyl费米子的产生和观测提供了新的思路和途径:在凝聚态体系中,某些低能元激发跟Weyl费米子的行为一致,有可能取得突破,首次实现Weyl电子态。最近几年来,如何在凝聚态物质中实现Weyl电子态成为该领域一个很具挑战性的科学问题,也是该领域国际竞争的焦点之一。
突破首先来自拓扑狄拉克半金属的发现。在该电子态中,两个手性相反的Weyl费米子在动量空间中重叠出现。中科院物理所方忠、戴希、翁红明及合作者于2012年和2013年先后从理论上预言Na3Bi[1]和Cd3As2[2]是狄拉克半金属,其费米面由四度简并的狄拉克点构成,是无质量的狄拉克费米子。2014年,他们跟实验组合作,分别在Na3Bi[3]和Cd3As2[4]中观测到了三维狄拉克锥,证实了理论预言,被称为首次发现“三维石墨烯”。(见2014年科研动态第2期)随后,众多的实验和理论工作迅速开展,已经形成了当前凝聚态领域的一个研究热点。
把狄拉克半金属中重叠的手性相反的Weyl费米子在动量空间中分开就可以实现真正的Weyl半金属态。这需要打破能带的自旋简并,通常可以通过破缺时间反演或中心反演对称来实现。2011年,中科院物理所方忠、戴希、翁红明等理论上预言HgCr2Se4的基态就是铁磁Weyl半金属态(见2011年科研动态第35期),但是由于磁性材料中复杂的磁畴结构,以及角分辨光电子能谱(ARPES)对磁场的屏蔽要求等,使得磁性Weyl半金属的实验观测变得极其困难。
最近,翁红明、方忠、戴希等一起,通过第一性原理计算,发现TaAs,TaP,NbAs和NbP等同结构家族材料是天然存在的,非磁性非中心对称的Weyl半金属。图1显示TaAs家族材料呈体心四方结构,其晶格动量空间存在12对手性相反的Weyl费米子。图2显示 Weyl点附近的贝里曲率呈刺猬状分布,与实空间中点电荷产生的电场分布类似,表明它们是动量空间中的磁单极子[5]。在TaAs的(001)表面上,会出现连接不同手性Weyl费米子投影的费米弧,能被ARPES实验直接观测到。
由于TaAs等样品的合成和测量实际可行,该工作2014年底在 arXiv网站公开后(arXiv:1501.00060,已发表于Phys. Rev. X5,011029 (2015)),受到了热切关注。许多研究组迅速开展了实验验证工作。在这几个月内,就已经有近8个实验工作证实了这个理论预言。中科院物理所的实验小组在这场竞赛中做出了许多重要的工作。例如首次观测到了TaAs的表面费米弧[arxiv:1502.04684]、由“手性异常”导致的负磁阻现象[arxiv:1503.01304]、Weyl点及其附近的三维狄拉克锥等[arxiv:1503.09188]。这是自1929年Weyl费米子被提出以来,首次在凝聚态物质中实现Weyl电子态并观测到其特有的物理特性,具有非常重要的物理意义。Weyl半金属的发现不仅给我们提出了很多新的科学问题,同时也带来了未来革新性技术突破的希望。在Weyl半金属中,由于受到拓扑保护,两个具有相反手性的Weyl电子态之间的散射很弱,可以用于实现极低能耗的电子输运。特别是该电子态可以在室温下稳定存在,对室温低能耗电子学器件的应用具有重要价值。
本工作得到了国家自然科学基金委(No. 11274359,No. 11422428),科技部973项目(No. 2011CBA00108,No. 2013CB921700)和中国科学院先导B项目(No. XDB07020100)的支持。
[1] Z. Wang, Y. Sun, X. Q. Chen, C. Franchini, G. Xu, H. Weng, X. Dai and Z. Fang, Phys. Rev. B 85, 195320 (2012).
[2] Z. Wang, H. Weng, Q. Wu, X. Dai and Z. Fang, Phys. Rev. B 88, 125427 (2013).
[3] Z. Liu et al. Science 343, 864 (2014).
[4] Z. Liu et al. Nat. Mater. 13, 677 (2014).
[5] Z. Fang et al. Science 302, 92 (2003).
突破首先来自拓扑狄拉克半金属的发现。在该电子态中,两个手性相反的Weyl费米子在动量空间中重叠出现。中科院物理所方忠、戴希、翁红明及合作者于2012年和2013年先后从理论上预言Na3Bi[1]和Cd3As2[2]是狄拉克半金属,其费米面由四度简并的狄拉克点构成,是无质量的狄拉克费米子。2014年,他们跟实验组合作,分别在Na3Bi[3]和Cd3As2[4]中观测到了三维狄拉克锥,证实了理论预言,被称为首次发现“三维石墨烯”。(见2014年科研动态第2期)随后,众多的实验和理论工作迅速开展,已经形成了当前凝聚态领域的一个研究热点。
把狄拉克半金属中重叠的手性相反的Weyl费米子在动量空间中分开就可以实现真正的Weyl半金属态。这需要打破能带的自旋简并,通常可以通过破缺时间反演或中心反演对称来实现。2011年,中科院物理所方忠、戴希、翁红明等理论上预言HgCr2Se4的基态就是铁磁Weyl半金属态(见2011年科研动态第35期),但是由于磁性材料中复杂的磁畴结构,以及角分辨光电子能谱(ARPES)对磁场的屏蔽要求等,使得磁性Weyl半金属的实验观测变得极其困难。
最近,翁红明、方忠、戴希等一起,通过第一性原理计算,发现TaAs,TaP,NbAs和NbP等同结构家族材料是天然存在的,非磁性非中心对称的Weyl半金属。图1显示TaAs家族材料呈体心四方结构,其晶格动量空间存在12对手性相反的Weyl费米子。图2显示 Weyl点附近的贝里曲率呈刺猬状分布,与实空间中点电荷产生的电场分布类似,表明它们是动量空间中的磁单极子[5]。在TaAs的(001)表面上,会出现连接不同手性Weyl费米子投影的费米弧,能被ARPES实验直接观测到。
由于TaAs等样品的合成和测量实际可行,该工作2014年底在 arXiv网站公开后(arXiv:1501.00060,已发表于Phys. Rev. X5,011029 (2015)),受到了热切关注。许多研究组迅速开展了实验验证工作。在这几个月内,就已经有近8个实验工作证实了这个理论预言。中科院物理所的实验小组在这场竞赛中做出了许多重要的工作。例如首次观测到了TaAs的表面费米弧[arxiv:1502.04684]、由“手性异常”导致的负磁阻现象[arxiv:1503.01304]、Weyl点及其附近的三维狄拉克锥等[arxiv:1503.09188]。这是自1929年Weyl费米子被提出以来,首次在凝聚态物质中实现Weyl电子态并观测到其特有的物理特性,具有非常重要的物理意义。Weyl半金属的发现不仅给我们提出了很多新的科学问题,同时也带来了未来革新性技术突破的希望。在Weyl半金属中,由于受到拓扑保护,两个具有相反手性的Weyl电子态之间的散射很弱,可以用于实现极低能耗的电子输运。特别是该电子态可以在室温下稳定存在,对室温低能耗电子学器件的应用具有重要价值。
本工作得到了国家自然科学基金委(No. 11274359,No. 11422428),科技部973项目(No. 2011CBA00108,No. 2013CB921700)和中国科学院先导B项目(No. XDB07020100)的支持。
[1] Z. Wang, Y. Sun, X. Q. Chen, C. Franchini, G. Xu, H. Weng, X. Dai and Z. Fang, Phys. Rev. B 85, 195320 (2012).
[2] Z. Wang, H. Weng, Q. Wu, X. Dai and Z. Fang, Phys. Rev. B 88, 125427 (2013).
[3] Z. Liu et al. Science 343, 864 (2014).
[4] Z. Liu et al. Nat. Mater. 13, 677 (2014).
[5] Z. Fang et al. Science 302, 92 (2003).
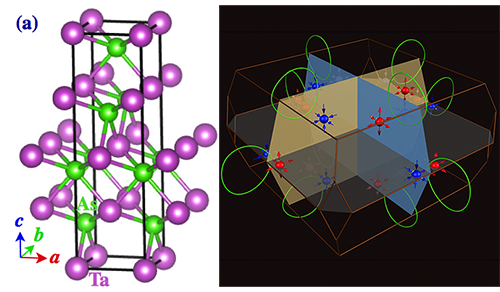 |
| 图一、TaAs晶体结构和Weyl费米子在动量空间的分布。 |
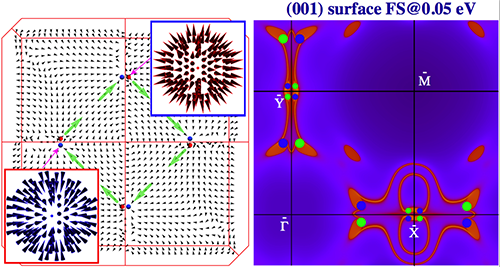 |
| 图二, Weyl点附近贝里曲率分布和(001)表面上连接相反磁荷投影点的费米弧。 |

