拓扑材料的发现对新的拓扑态和新奇物性的研究具有重要的意义。不久前,通过拓扑量子化学[1],对称性指标[2,3]等手段对无机晶体材料做了地毯式的搜索和分类,可以通过开源程序(https://github.com/zjwang11/irvsp)判别任何非磁晶体材料的拓扑性质 (www.cryst.ehu.es/cryst/checktopologicalmat)[4]。高阶拓扑绝缘体(higher-order topological insulators) 在这次搜索中也无处遁形。 人们定义: 一阶拓扑绝缘体具有绝缘的d维体态,但有(d-1)维拓扑保护的金属表面态; 二阶拓扑绝缘体具有绝缘的d维体态和(d-1)维表面态,但有(d-2)维拓扑保护的金属棱态;以此类推。所以常规的三维拓扑绝缘体,又可以被称为三维的一阶拓扑绝缘体。物理系统中的对称性一直可以大大的简化我们的研究,比如三维(一阶)拓扑绝缘体在有中心反演的情况下,其Fu-Kane Z2拓扑指标可以简化为所有占据态八个时间反演不变点奇宇称能带的对数的总和,再对二取余。这样我们就知道,对于有中心反演的体系,不同宇称的能带在时间反演不变点发生一次能带反转(band inversion,简称“反带”),就可以得到拓扑节线半金属(不考虑自旋轨道耦合SOC)和拓扑绝缘体(考虑SOC)。如果同样的反带发生两次(double band inversion),如图一所示,虽然它对应的Fu-Kane Z2拓扑指标都是零, 但是拓扑量子化学以及后来发展的等价的对称性指标都显示它是拓扑非平庸的。
近日,中国科学院物理研究所/北京凝聚态物理国家研究中心王志俊特聘研究员,与美国普林斯顿大学的博士后Benjamin J. Wieder和B. Andrei Bernevig教授等人合作,通过第一性原理计算,发现β相的过渡金属碲化物MoTe2就处在这个非平庸相,它又称为三维的二阶拓扑绝缘体,由基于中心反演对称性的拓扑数Z4=2描述[5]。在不考虑SOC的情况下,这样的二次反带得到的是一个Z2非平庸的拓扑节线半金属(monopole nodal line sem-imetal)。这个概念早在2015年由物理所方辰研究员提出,却一直鲜有材料实现。在考虑SOC之后,它实际上是三维的二阶拓扑绝缘体,即具有绝缘的体态和表面态(k点处处有能隙),但具有helical的时间反演保护的金属棱态。同时,该项研究也解决了这一系列材料中γ相的MoTe2、WTe2中表面态的起源问题:这些比较大的表面态并不是拓扑平庸的,而是两个狄拉克锥表面态(图二a,b,c)杂化之后的产物,属于高阶拓扑绝缘体在表面上的反映(图二d,e)。
这项工作近期发表在Phys. Rev. Lett. 123, 186401 (2019)上,图2e被选为同期PRL杂志封面。参与该工作合作研究的还包括西湖大学李牮博士和魏茨曼科学研究院颜丙海研究员。此项工作得到国家自然科学基金委支持。
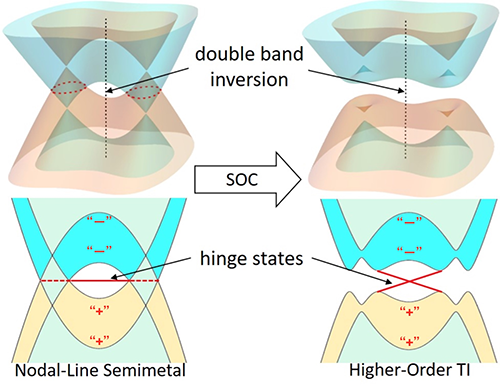 |
| 图一: 在同时具有时间反演和中心反演的体系中,不同宇称的能带反带两次(double band inversion)得到的拓扑态由Z4=2来描述。在不考虑自旋轨道耦合(SOC)的情况下,体系可以形成携带拓扑非平庸的Z2拓扑荷的节线(monopole nodal lines),对应的棱态是一个类似石墨烯zigzag边的平带。在考虑SOC之后,它对应的体态和表面态都会打开能隙,但是在棱上会形成helical的一维金属态,其交叉点受时间反演对称性保护。 |
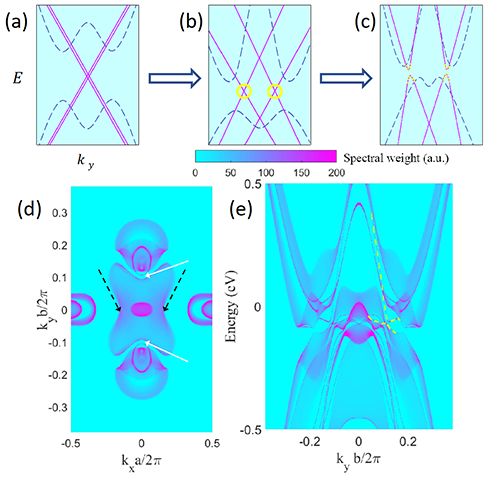 |
| 图二:(a)-(c)表示由两次反带形成的两个表面Dirac锥的演化,杂化后打开能隙。 实际材料β-MoTe2中,(001)表面上的费米面 (d)和表面态沿着ky的色散(e)。 |
[1] Barry Bradlyn et al., "Topological quantum chemistry", Nature, 547 (2017).
[2] Po, H. C. et al., "Symmetry-based indicators of band topology in the 230 space groups", Nat. Comm. 8, 50 (2017).
[3] Z. Song et al., "Quantitative mappings between symmetry and topology in solids", Nat. Comm. 9, 3530 (2018).
[4] Vergniory, M.G., et al., “A complete catalogue of high-quality topological materials”, Nature, 566, 480-485 (2019).
[5] Zhijun Wang et al., Phys. Rev. Lett. 123, 186401 (2019).

