在复杂系统中寻找最优方案一直是科学与工程领域里的挑战难题之一。以旅行商问题为代表的组合优化任务广泛出现在物流运输、网络设计及人工智能等领域。然而,随着问题规模增大,经典确定性算法往往难以兼顾效率与质量,而引入随机性的启发式方法又受到随机数质量与可调控性的限制。如何在硬件层面获得高质量、可配置的随机性,并将其有效嵌入求解过程,是该类问题长期面临的关键科学问题。
近期,中国科学院物理研究所/北京凝聚态物理国家研究中心科研人员基于磁性隧道结的物理随机性,提出了一种面向组合优化任务的概率贪心求解框架,实现了在硬件层面上的可调分布真随机数驱动下对旅行商问题的高效优化求解。磁性隧道结在外加脉冲自旋极化电流作用下其自由层磁矩呈现固有的180度随机翻转行为,其翻转概率通过脉冲电压幅值或宽度等参数可连续精确调控。利用这一特性构建可配置概率分布的真随机数发生器,并将其嵌入优化算法中,使得算法基于当前系统状态对下一步选择的概率分布能够实时更新与重构,从而在“局部选择”与“全局探索”间实现动态平衡。
在实验层面,该项研究利用多个磁性隧道结器件演示生成满足高斯、均匀、指数以及用户自定义概率分布的真随机数,并系统验证了其统计特性、可重复性以及分布可调性。进一步,这些可调分布真随机数被用于驱动概率贪心算法对旅行商问题进行硬件求解。在求解经典的Burma14基准问题中,该方法获得的路径长度显著优于传统贪心算法,并可通过调节等效温度参数快速实现最优解附近的高概率采样。值得注意的是,该方法仅需数量随对数增长(log₂N, N为城市数)的磁性隧道结器件即可完成对任意目标概率分布的编码,配合脉冲电压宽度调制与自校准机制,可在无需高精度模拟电路支持的条件下保持输出概率的长期稳定性。这一特性使其具备面向大规模片上优化加速器应用的潜在优势。此外,该方法逐步采样并动态更新概率分布的过程,与大型语言模型在内容生成过程中逐个词元(Token)采样的机制高度相似,展现了面向未来人工智能推理的硬件级随机性加速方案的可行性。
基于磁性隧道结的可配置概率分布的真随机源为求解组合优化问题提供了新的物理实现路径,有望推动面向低功耗、高效率的概率计算硬件的发展。该工作也为基于物理随机性的求解框架提供了新思路,为未来自旋电子学器件在智能计算中的应用开辟了可行路径。该项研究成果以“Probabilistic Greedy Algorithm Solver Using Magnetic Tunneling Junctions for Traveling Salesman Problem”为题发表在Nature Communications期刊(https://doi.org/10.1038/s41467-025-66864-9),中国科学院物理研究所M02组博士毕业生张然为第一作者,中国科学院物理研究所韩秀峰研究员、万蔡华副研究员和德国弗劳恩霍夫协会的Thomas Kämpfe教授为共同通讯作者,该项研究得到了国家重点研发项目(MOST)、国家自然科学基金(NSFC)和中国科学院国际交流计划(PIFI)的资助。
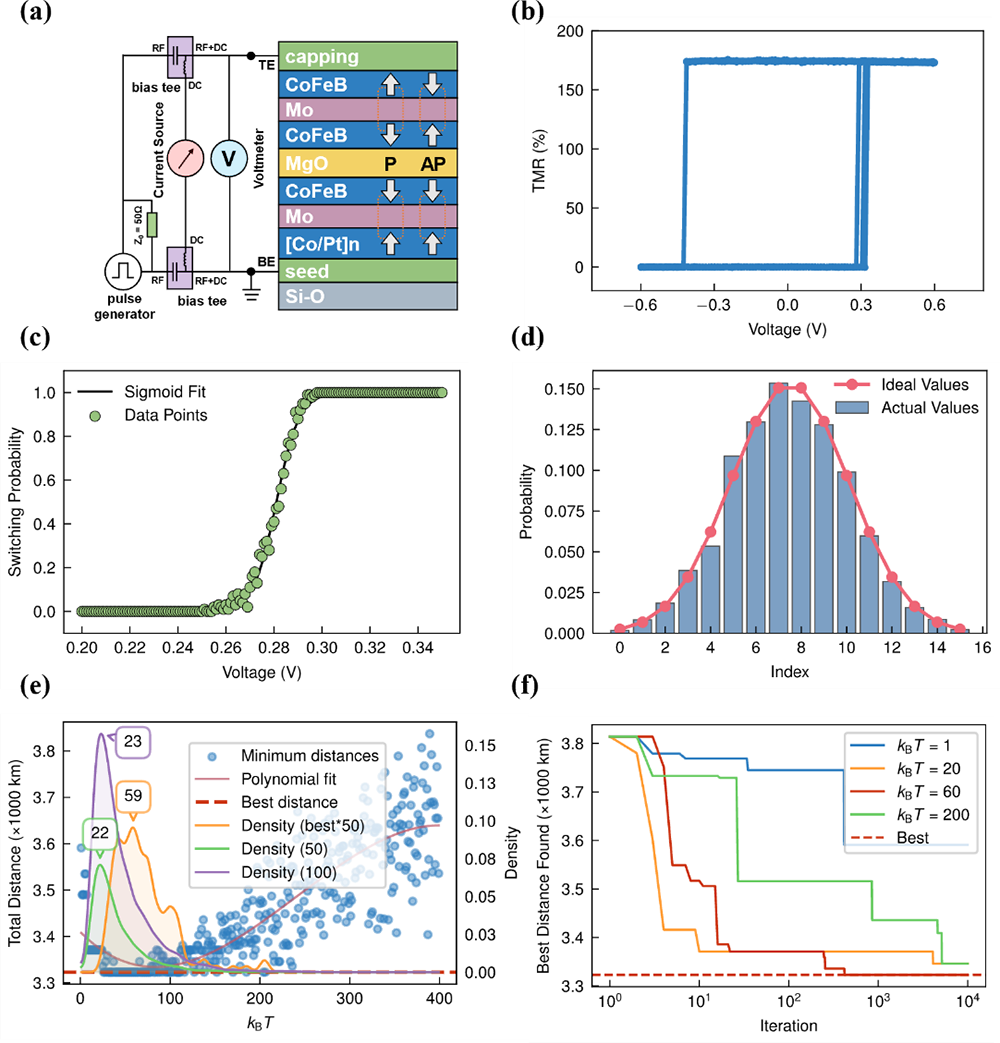
图:基于磁性隧道结的概率分布可调真随机数发生器及概率贪心算法求解器示意图。(a) 器件结构与测量系统的示意图。(b) 由脉冲电流触发自由层磁矩翻转所表现出的磁性隧道结隧穿磁电阻(TMR)高低变化行为。(c) 磁性隧道结的磁矩翻转概率随写入电压变化的关系曲线,黑色实线为拟合得到的S形函数。(d) 由磁性隧道结真随机数发生器生成并呈现高斯分布的随机数。(e) 不同温度kBT取值(1至400)下获得的最优解散点图(左)以及在最优解附近0、50和100千米内的解空间密度分布图(右)。每个密度图基于概率贪心算法的100次独立求解结果。(f) 在四组kBT取值下最优路径长度随迭代次数的变化关系。当kBT = 60时可在约1000次迭代内获得最优解。

